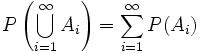Podstawy teorii weryfikacji hipotez statystycznych

Hipoteza statystyczna to dowolne przypuszczenie dotyczące rozkładu populacji - postaci funkcyjnej lub wartości parametru rozkładu. Proces sprawdzenia prawdziwości tego przypuszczenia na podstawie wyników próby losowej to weryfikacja hipotez statystycznych.
Formułowanie hipotezy statystycznej rozpoczyna się zebranianiem informacji na temat populacji i jej możliwego rozkładu. Dzięki temu możliwe jest zbudowanie zbioru hipotez dopuszczalnych Ω, czyli zbioru rozkładów, które mogą charakteryzować badaną populację. Hipoteza statystyczna to każdy podzbiór zbioru hipotez dopuszczalnych.
Podział hipotez statystycznych
Hipotezy statystyczne można podzielić na:

• parametryczne - hipoteza dotyczy wartości parametru rozkładu
• nieparametryczne - hipoteza dotyczy postaci funkcyjnej rozkładu

Według innego kryterium podział przebiega następująco:

• proste - hipoteza jednoznacznie określa rozkład danej populacji, czyli odpowiadający jej podzbiór zbioru Ω zawiera jeden element (rozkład)
• złożone - hipoteza określa całą grupę rozkładów, zaś odpowiadający jej podzbiór
• zbioru Ω zawiera więcej niż jeden element
• alternatywna - przyjmujemy ją kiedy odrzucamy hipotezę zerową

Weryfikacja hipotez parametrycznych Przykład Należy dokonać oceny partii pudelek zapalek liczącej 100 tys. sztuk. dostawca twierdzi, że w pudelku znajdują się przecietnie 54 zapalki. Zweryfikować hipotezę H0(m = m0 = 54). Ponieważ nie znamy rozkładu liczby zapałek w pudełkach w populacji generalnej, a mozemy łatwo pobrać próbę >= 30 możemy wieć w przybliżeniu skorzystać z rozkładu normalnego. Zkaldamy, że przy próbie o wielkości n = 100 odnotowano średnią arytmetyczną mn = 51,21 natomiast σn' = 2,54. Weryfikujemy przy poziomie istotności α = 0,02 ponieważ obraliśmy dużą próbę więc . Musimy zatem wyznaczyć t dla ktorego
Definiujemy unormowaną zmienną Y:
podstawiamy do wzoru

Z własności bezwzględnej wartości:

Ponieważ funkcja gęstości jest dla rozkładu N(0,1) parzysta to zachodzi równość:

Wiadomo, że P(A) to to samo co 1-P(A') więc:
1 − P(Y < t) = 0,01
P(Y < t) = 0,99
A P(Y F(t) = 0,99
Teraz w tablicy rozkładu normalnego znajdujemy najmniejszą wartość t dla której F(t) wynosi conajmniej 0,99. Jest to wartość 2,33.
Hipotezę H0 należy wiec odrzucić na poziomie istotności α jeżeli w przeciwnym wypadku przy zadanej istotności α = 0,02 nie możemy ani potwierdzić hipotezy, ani jej odrzucić.
Zgodnie z naszymi danymi wychodzi:
| Mn − 54 | = | 51,21 − 54 | = 2,79

Więc:

Zatem hipotezę możemy odrzucić (jeśli wyjdzie odwrotnie to piszemy że nie odrzucamy ani nie potwierdzamy - tak właśnie trzeba było zrobić na egzaminie, bo wychodziło <).

Testem statystycznym nazywamy każdą jednoznacznie zdefiniowaną regułę postępowania określającą warunki przy których należy weryfikowaną hipotezę przyjąć bądź odrzucić. Weryfikacja hipotez statystycznych odbywa się na podstawie wyników zaobserwowanych w próbie. W rezultacie test statystyczny podaje reguły, przy jakiego rodzaju wynikach próby sprawdzaną hipotezę się przyjmuje, a przy jakich odrzuca.
Weryfikowaną hipotezę nazywa się zwykle hipotezą zerową: H0
D e cy z j a
Hipoteza H0 Przyjąć H0 Odrzucić H0
Jest prawdziwa Decyzja poprawna Błąd I rodzaju. Prawdopodobieństwo popełnienia tego błędu.
Jest fałszywa Błąd II rodzaju Decyzja poprawna
Wartość prawdopodobieństwa popełnienia błędu I rodzaju - nazywamy poziomem istotności testu; najczęściej przyjmuje się = 0,05 , lub = 0,1.
Oprócz hipotezy zerowej formułujemy również hipotezę H1 ( hipotezę alternatywna), którą skłonni jesteśmy przyjąć, jeśli weryfikowaną hipotezę H0 należy odrzucić. Sprawdzian hipotezy jest to pewna funkcja wyników z próby, na podstawie której decydujemy, czy można hipotezę H0 przyjąć, czy odrzucić. Przez obszar krytyczny rozumie się taki zbiór wartości sprawdzianu hipotezy, że jeżeli zaobserwowana wartość sprawdzianu znajdzie się w tym obszarze, to odrzuca się hipotezę H0 na korzyść H1. Prawdopodobieństwo tego, że sprawdzian przyjmie wartość należącą do obszaru krytycznego, jest przy założeniu prawdziwości hipotezy H0 równe założonemu poziomowi istotności .
1. 1. Testy istotności dla wartości oczekiwanej (średniej)
Model 1. Załóżmy, że populacja generalna ma rozkład normalny N(m,) o nieznanej wartości średniej m oraz znanym odchyleniu standardowym . Z populacji tej wylosowano n elementową próbę w celu zweryfikowania hipotezy
H0: m = m0
wobec hipotezy alternatywnej H1: m  m0 ,
gdzie m0 jest pewną hipotetyczna wartością średniej w populacji.
Sprawdzianem hipotezy jest statystyka:
która przy założeniu prawdziwości hipotezy H0 ma rozkład normalny N(0, 1). Jeśli H0 jest prawdziwa, to wartość bezwzględna U nie powinna przekraczać wartości krytycznej u , odczytanej z tablic rozkładu normalnego przy ustalonym poziomie istotności . Jeżeli odchylenie standardowe  w populacji generalnej nie jest znane, to we wzorze (1) można je zastąpić odchyleniem standardowym s obliczonym z próby. jest to uzasadnione tylko wtedy, gdy próba jest duża: n > 30.
Model 2. Dla małych prób losowych (n  30) do sprawdzania hipotezy
H0: m = m0 wykorzystujemy statystykę:
Statystyka przy założeniu prawdziwości hipotezy H0 ma rozkład t Studenta o n-1 stopniach swobody.
1.2. Test istotności dla wariancji
Załóżmy, że populacja generalna ma rozkład normalny N(m,) o nieznanych parametrach wartości średniej m i odchyleniu standardowym . Z populacji tej wylosowano n elementową próbę w celu zweryfikowania hipotezy wobec hipotezy alternatywnej , gdzie jest pewną hipotetyczną wartością wariancji w populacji.
Sprawdzianem hipotezy jest statystyka:
Statystyka ta ma przy założeniu prawdziwości H0 – rozkład 2 o n-1 stopniach swobody.
2.3. Test istotności dla wskaźnika struktury
Na podstawie n-elementowej próby (n>100) weryfikujemy hipotezę :
H0: p = p0
wobec hipotezy alternatywnej:
H1: p  p0 ,
Sprawdzianem hipotezy jest statystyka:
która przy założeniu prawdziwości hipotezy H0 ma rozkład normalny N(0, 1), przy czym X oznacza ilość jednostek o wyróżnionej wartości cechy w n-elementowej próbie.

Wielkie układy równań liniowych

Wraz z coraz większymi modelami pojawiającymi się w praktyce obliczeniowej, coraz częściej zachodzi potrzeba rozwiązywania zadań algebry liniowej, w której macierze są co prawda wielkiego wymiaru, ale najczęściej rozrzedzone, to znaczy jest w nich bardzo dużo zer. Bardzo często zdarza się, że macierz wymiaru N ma tylko O(N) niezerowych elementów. Wykorzytanie tej specyficznej własności macierzy nie tylko prowadzi do algorytmów istotnie szybszych od ich analogów dla macierzy gęstych (to znaczy takich, które (w założeniu) mają N^2 elementów), ale wręcz są jedynym sposobem na to, by niektóre zadania w ogóle stały się rozwiązywalne przy obecnym stanie techniki obliczeniowej! Jednym ze szczególnie ważnych źródeł układów równań z macierzami rozrzedzonymi są np. równania różniczkowe cząstkowe (a więc np. modele pogody, naprężeń w konstrukcji samochodu, przenikania kosmetyków do głębszych warstw skóry, itp.). Modele wielostanowych systemów kolejkowych (np. routera obsługującego wiele komputerów) także prowadzą do gigantycznych układów równań z macierzami rozrzedzonymi o specyficznej strukturze. Z reguły zadania liniowe wielkiego wymiaru będą miały strukturę macierzy rozrzedzonej, gdyż najczęściej związki pomiędzy niewiadomymi w równaniu nie dotyczą wszystkich, tylko wybranej grupy.
więcej na temat wielkich układów równań liniowych

Wektory i wartości własne

Wektory i wartości własne – wielkości opisujące endomorfizm danej przestrzeni liniowej; wektor własny przekształcenia można rozumieć jako wektor, którego kierunek nie ulega zmianie po przyłożeniu do niego endomorfizmu; wartość własna odpowiadająca temu wektorowi to skala podobieństwa tych wektorów.
Najczęściej przekształcenie liniowe wyraża się jako macierz, która działa na wektory; wówczas stosuje się nazwy wektor własny macierzy, wartość własna macierzy. W innych teoriach przekształcenia i elementy przestrzeni liniowej mogą mieć inne nazwy. Mówi się wtedy przykładowo o stanach własnych operatora, funkcjach własnych funkcjonału itp.

DEFINICJE

Niech x będzie przestrzenią liniową nad ciałem K zaś T oznacza pewien jej endomorfizm, tzn. przekształcenie liniowe tej przestrzeni w siebie. Jeśli dla pewnego niezerowego wektora przestrzeni spełniony jest warunek

,
gdzie jest pewnym skalarem, to x nazywa się wektorem własnym, a nazywa się wartością własną przekształcenia T.
Danej wartości własnej operatora T odpowiada zbiór:

nazywany podprzestrzenią własną odpowiadającą wartości własnej

gdyż tworzy on domkniętą podprzestrzenią liniową przestrzeni X Jej wymiar nazywa się wielokrotnością wartości własnej.
Często zakłada się, że K jest ciałem liczb rzeczywistych bądź zespolona, zaś na X określona jest topologia liniowa. W zastosowaniach (np. równania różniczkowe) bada się często wartości własne operatorów liniowych określonych na przestrzeniach Banacha, Hilberta itp. W dalszej części artykułu będziemy zakładać ogólnie, że X jest pewną przestrzenią Banacha, a jest ustalonym operatorem liniowym i ciągłym.

WŁASNOŚCI

• Jeżeli T jest samosprzężonym operatorem liniowym na przestrzeni Hilberta X to wartości własne tego operatora są rzeczywiste, ponadto wektory własne, odpowiadające różnym wartościom własnym są ortogonalne.
• Jeżeli jest wartością własną operatora T to (założenie zupełności przestrzeni jest tu nieistotne).
• Liczba jest wartością własną operatora T wtedy i tylko wtedy, gdy operator nie jest różnowartościowy.
• Wektory własne odpowiadające różnym wartościom własnym są liniowo niezależne.
• Jeśli macierz A potraktować jako macierz przekształcenia liniowego pewnej przestrzeni liniowej V to wektory własne odpowiadające tej samej wartości własnej tworzą podprzestrzeń.
• Jeśli suma wymiarów podprzestrzeni z powyższej własności jest równa wymiarowi V to wektory własne odpowiadające różnym wartościom własnym tworzą bazę tej przestrzeni

PRZYKŁADY:

Przestrzenie skończeniewymiarowe
Przekształcenie liniowe A skończeniewymiarowych przestrzeni liniowych z ustalonymi bazami można przedstawić za pomocą macierzy A nazywanej macierzą przekształcenia liniowego.
Endomorfizmowi A na skończeniewymiarowej przestrzeni X odpowiada macierz kwadratowa A, a jej wartości własne są pierwiastkami jej wielomianu charakterystycznego

gdzie I jest macierzą jednostkową.
Mając do dyspozycji wartości własne można obliczyć odpowiadające im wektory własne rozwiązując równania postaci

ze względu na wektory Xi. Zbiór wszystkich wartości własnych operatora tworzy widmo punktowe operatora; w szczególności, gdy operator jest reprezentowany przez macierz, to mówi się o widmie macierzy. Jeżeli macierz A jest symetryczna, to wszystkie jej wartości własne są liczbami rzeczywistymi. Transponowanie macierzy nie zmienia jej wartości własnych.
Równanie całkowe jednorodne Fredholma
Niech będzie przestrzenią funkcji całkowalnych z kwadratem w sensie Lebesgue'a na przedziale (a,b) oraz niech K(s,t) będzie będzie funkcją całkowalną z kwadratem w zbiorze

Można wykazać, że odwzorowanie dane wzorem

jest operatorem liniowym i ciągłym, przy czym, gdy , to T jest operatorem samosprzężonym, a zatem ma wyłącznie rzeczywiste wartości własne.

Rachunek prawdopodobieństwa

Rachunek Prawdopodobieństwa - dział matematyki zajmujący się zdarzeniami losowymi. Rachunek prawdopodobieństwa zajmuje się badaniem abstrakcyjnych pojęć matematycznych stworzonych do opisu zjawisk, które nie są deterministyczne: zmiennych losowych w przypadku pojedynczych zdarzeń oraz procesów stochastycznych w przypadku zdarzeń powtarzających się (w czasie). Jako matematyczny fundament statystyki, teoria prawdopodobieństwa odgrywa istotną rolę w sytuacjach, w których konieczna jest analiza dużych zbiorów danych. Jednym z największych osiągnięć fizyki dwudziestego wieku było odkrycie probabilistycznej natury zjawisk fizycznych w skali mikroskopijnej, co zaowocowało powstaniem mechaniki kwantowej.
Matematyczna teoria prawdopodobieństwa sięga swoimi korzeniami do analizy gier losowych podjętej w siedemnastym wieku przez Pierre de Fermata oraz Blaise Pascala. Z tego powodu, początkowo teoria prawdopodobieństwa zajmowała się niemal wyłącznie zjawiskami dyskretnymi i używała metod kombinatorycznych. Zmienne ciągłe zostały wprowadzone do teorii prawdopodobieństwa znacznie później. Za początek stworzenia współczesnej teorii prawdopodobieństwa powszechnie uważa się jej aksjomatyzację, której w 1933 dokonał Andriej Kołmogorow. Współczesna teoria prawdopodobieństwa jest ściśle związana z teorią miary.
Pomimo że wynik pojedynczego rzutu monetą lub kością do gry często z praktycznego punktu widzenia można uważać za nieprzewidywalny, jeżeli eksperyment taki powtórzony zostaje wielokrotnie, mogą pojawić się pewne prawidłowości i wzory statystyczne, które można badać i przewidzieć. Dwa przykłady takich prawidłowości, i kluczowe osiągnięcia rachunku prawdopodobieństwa, to prawo wielkich liczb oraz centralne twierdzenie graniczne.

DEFINICJA PRAWDOPODOBIEŃSTWA
Prawdopodobieństwem nazywamy dowolną funkcję P o wartościach rzeczywistych, określoną na σ-ciele zdarzeń , spełniającą warunki:
1. dla każdego ;
2. ;
3. Jeśli oraz dla , to

Warunki (1-3) zostały sformułowane przez Kołmogorowa w roku 1933 jako aksjomaty teorii prawdopodobieństwa. Matematyczny model doświadczenia losowego to trójka

gdzie P jest prawdopodobieństwem, określonym na pewnym σ-ciele F podzbiorów zbioru zdarzeń elementarnych omega. Trójkę tę nazywamy przestrzenią probabilistyczną.

Schemat Bernoulliego

Wśród doświadczeń wieloetapowych na szczególną uwagę zasługuję te, które polegają na n-krotnym powtórzeniu, w tych samych warunkach i niezależnie od siebie doświadczenia losowego, kończącego się tylko jednym z dwóch możliwych wyników. Takie doświadczenie nazywamy próbą Bernoullioego. Przykładem próby Bernoulliego jest: rzut monetą (orzeł, reszka), kupno losu na loterii (los wygrany, los przegrany).
Wielokrotne powtórzenie próby nazwiemy niezależnymi, jeśli pojawienie się dowolnych wyników w jednej próbie nie zmienia prawdopodobieństwa pojawienia się wyników przy pozostałych próbach.
Jeżeli przeprowadzimy n niezależnych i identycznych doświadczeń, w których są tylko dwa możliwe wyniki, to taki ciąg powtórzeń tego samego doświadczenia nazywamy schematem Bernoulliego. W schemacie tym jedno ze zdarzeń elementarnych nazywamy sukcesem, a drugie porażką.
W schemacie n prób Bernoulliego prawdopodobieństwo Pn(k) otrzymania dokładnie k sukcesów wyraża się wzorem:

,
gdzie p jest prawdopodobieństwem sukcesu, zaś q = 1 - p prawdopodobieństwem porażki w próbie Bernoulliego, przy czym 0 < p < 1, k = 0, 1, 2, ..., n.

Najbardziej prawdopodobna liczba sukcesów w schemacie Bernoulliego
Jeśli (n + 1)p nie jest liczbą całkowitą, to najbardziej prawdopodobną liczbą sukcesów w schemacie n prób Bernoulliego, jest największa liczba całkowita mniejsza od (n + 1)p. Jeśli natomiast (n + 1)p jest liczbą całkowitą, to najbardziej prawdopodobne są dwie wartości: (n + 1)p - 1 oraz (n + 1)p.

Test z http://wazniak.mimuw.edu.pl/index.php?title=Rachunek_prawdopodobie%C5%84stwa_i_statystyka/Test_5:_Prawdopodobie%C5%84stwo_warunkowe_i_niezale%C5%BCno%C5%9B%C4%87

Układy równań liniowych

Układ równań liniowych – koniunkcja pewnej liczby (być może nieskończonej[1]) równań liniowych, czyli równań pierwszego rzędu. Teoria układów równań liniowych jest działem algebry liniowej leżącej u podstaw nowoczesnej matematyki. Algorytmami obliczeniowymi zajmuje się dział nazywany numeryczna algebra liniowa, same zaś metody odgrywają ważną rolę w inżynierii, fizyce, chemii, informatyce i ekonomii. Częstokroć aproksymuje (przybliża) się bardziej skomplikowane układy równań nieliniowych (opisujące modele matematyczne, czy symulacje komputerowe) dużo prostszymi układami równań liniowych (tzw. linearyzacja). Układy równań liniowych rozpatruje się najczęściej nad ciałami (np. liczbami wymiernymi, rzeczywistymi, czy zespolonymi); choć ma to sens już w przypadku pierścieni (np. liczb całkowitych), to rozwiązywanie takich układów nastręcza znacznie więcej trudności (w szczególności oznacza to badanie modułów zamiast przestrzeni liniowych, zob. uogólnienia). W dalszej części przyjmuje się, że wszystkie współczynniki należą do ustalonego ciała.
Motywacje
W geometrii euklidesowej można rozpatrywać miejsca geometryczne wyznaczone przez dane dwie proste na płaszczyźnie – mogą one wyznaczać prostą, punkt lub nie wyznaczać żadnego miejsca geometrycznego; odpowiada im odpowiednio nieskończony zbiór elementów, zbiór złożony z pojedynczego elementu lub zbiór pusty. Wprowadzenie na płaszczyźnie układu współrzędnych umożliwia algebraizację tego zadania: proste zadane są za pomocą równań liniowych, zaś miejsce geometryczne wyznaczone przez te proste odpowiada zbiorowi elementów spełniających wszystkie równania jednocześnie.
Jeśli w układzie współrzędnych kartezjańskich proste zadane są równaniami

oraz

to ich jedyny punkt wspólny (x0,y0) ma współrzędne (2,3) co łatwo sprawdzić wprost:


To że jest to jedyny punkt wynika z faktu, iż proste te nie są równoległe. Zwyczajowo równania prostych zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
nazywając je układem równań liniowych, zaś zbiór elementów spełniających każde równanie z osobna (odpowiadający punktom wspólnym prostych) – jego rozwiązaniami.

Rozwiązaniem układu równań x-y=-1 oraz 3x+y=9 jest para uporządkowana (2,3) gdyż podstawienie do równań poprzednika tej pary za x i jej następnika za y da dwie tożsamości.







Rozwiązania
Rozwiązaniem U nazywa się dowolny ciąg liczb ri który po podstawieniu za xj będzie spełniał każde z równań U. Układ, który nie ma rozwiązań, nazywa się sprzecznym; jeżeli zbiór rozwiązań układu jest niepusty, to nazywa się go niesprzecznym. Układ niesprzeczny, który ma jedno i tylko jedno rozwiązanie, nazywa się oznaczonym; układy o więcej niż jednym rozwiązaniu nazywa się nieoznaczonymi – w przypadku układów liniowych nad ciałami nieskończonymi (takimi jak liczby wymierne, liczby rzeczywiste, czy liczby zespolone) oznacza to, że układ ma nieskończenie wiele rozwiązań.
Wskazówkę co do ogólnej liczby rozwiązań układu daje już sama jego postać:
układ niedookreślony, który ma mniej równań niż niewiadomych, zwykle jest nieoznaczony;
układ nadokreślony mający więcej równań niż niewiadomych, zazwyczaj jest sprzeczny;
układ, który ma tyle równań co niewiadomych, często ma jedno rozwiązanie.
Przypadki te obrazują następujące wykresy dla układów równań liniowych dwóch zmiennych:

Zbiór rozwiązań dwóch równań liniowych o trzech zmiennych zwykle tworzy prostą (przestrzeń jednowymiarową).

Układ równań liniowych o trzech zmiennych określa zbiór płaszczyzn - dowolny ich punkt przecięcia (o ile istnieje) jest rozwiązaniem układu.