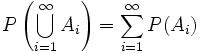Wektory i wartości własne

Wektory i wartości własne – wielkości opisujące endomorfizm danej przestrzeni liniowej; wektor własny przekształcenia można rozumieć jako wektor, którego kierunek nie ulega zmianie po przyłożeniu do niego endomorfizmu; wartość własna odpowiadająca temu wektorowi to skala podobieństwa tych wektorów.
Najczęściej przekształcenie liniowe wyraża się jako macierz, która działa na wektory; wówczas stosuje się nazwy wektor własny macierzy, wartość własna macierzy. W innych teoriach przekształcenia i elementy przestrzeni liniowej mogą mieć inne nazwy. Mówi się wtedy przykładowo o stanach własnych operatora, funkcjach własnych funkcjonału itp.

DEFINICJE

Niech x będzie przestrzenią liniową nad ciałem K zaś T oznacza pewien jej endomorfizm, tzn. przekształcenie liniowe tej przestrzeni w siebie. Jeśli dla pewnego niezerowego wektora przestrzeni spełniony jest warunek

,
gdzie jest pewnym skalarem, to x nazywa się wektorem własnym, a nazywa się wartością własną przekształcenia T.
Danej wartości własnej operatora T odpowiada zbiór:

nazywany podprzestrzenią własną odpowiadającą wartości własnej

gdyż tworzy on domkniętą podprzestrzenią liniową przestrzeni X Jej wymiar nazywa się wielokrotnością wartości własnej.
Często zakłada się, że K jest ciałem liczb rzeczywistych bądź zespolona, zaś na X określona jest topologia liniowa. W zastosowaniach (np. równania różniczkowe) bada się często wartości własne operatorów liniowych określonych na przestrzeniach Banacha, Hilberta itp. W dalszej części artykułu będziemy zakładać ogólnie, że X jest pewną przestrzenią Banacha, a jest ustalonym operatorem liniowym i ciągłym.

WŁASNOŚCI

• Jeżeli T jest samosprzężonym operatorem liniowym na przestrzeni Hilberta X to wartości własne tego operatora są rzeczywiste, ponadto wektory własne, odpowiadające różnym wartościom własnym są ortogonalne.
• Jeżeli jest wartością własną operatora T to (założenie zupełności przestrzeni jest tu nieistotne).
• Liczba jest wartością własną operatora T wtedy i tylko wtedy, gdy operator nie jest różnowartościowy.
• Wektory własne odpowiadające różnym wartościom własnym są liniowo niezależne.
• Jeśli macierz A potraktować jako macierz przekształcenia liniowego pewnej przestrzeni liniowej V to wektory własne odpowiadające tej samej wartości własnej tworzą podprzestrzeń.
• Jeśli suma wymiarów podprzestrzeni z powyższej własności jest równa wymiarowi V to wektory własne odpowiadające różnym wartościom własnym tworzą bazę tej przestrzeni

PRZYKŁADY:

Przestrzenie skończeniewymiarowe
Przekształcenie liniowe A skończeniewymiarowych przestrzeni liniowych z ustalonymi bazami można przedstawić za pomocą macierzy A nazywanej macierzą przekształcenia liniowego.
Endomorfizmowi A na skończeniewymiarowej przestrzeni X odpowiada macierz kwadratowa A, a jej wartości własne są pierwiastkami jej wielomianu charakterystycznego

gdzie I jest macierzą jednostkową.
Mając do dyspozycji wartości własne można obliczyć odpowiadające im wektory własne rozwiązując równania postaci

ze względu na wektory Xi. Zbiór wszystkich wartości własnych operatora tworzy widmo punktowe operatora; w szczególności, gdy operator jest reprezentowany przez macierz, to mówi się o widmie macierzy. Jeżeli macierz A jest symetryczna, to wszystkie jej wartości własne są liczbami rzeczywistymi. Transponowanie macierzy nie zmienia jej wartości własnych.
Równanie całkowe jednorodne Fredholma
Niech będzie przestrzenią funkcji całkowalnych z kwadratem w sensie Lebesgue'a na przedziale (a,b) oraz niech K(s,t) będzie będzie funkcją całkowalną z kwadratem w zbiorze

Można wykazać, że odwzorowanie dane wzorem

jest operatorem liniowym i ciągłym, przy czym, gdy , to T jest operatorem samosprzężonym, a zatem ma wyłącznie rzeczywiste wartości własne.

Rachunek prawdopodobieństwa

Rachunek Prawdopodobieństwa - dział matematyki zajmujący się zdarzeniami losowymi. Rachunek prawdopodobieństwa zajmuje się badaniem abstrakcyjnych pojęć matematycznych stworzonych do opisu zjawisk, które nie są deterministyczne: zmiennych losowych w przypadku pojedynczych zdarzeń oraz procesów stochastycznych w przypadku zdarzeń powtarzających się (w czasie). Jako matematyczny fundament statystyki, teoria prawdopodobieństwa odgrywa istotną rolę w sytuacjach, w których konieczna jest analiza dużych zbiorów danych. Jednym z największych osiągnięć fizyki dwudziestego wieku było odkrycie probabilistycznej natury zjawisk fizycznych w skali mikroskopijnej, co zaowocowało powstaniem mechaniki kwantowej.
Matematyczna teoria prawdopodobieństwa sięga swoimi korzeniami do analizy gier losowych podjętej w siedemnastym wieku przez Pierre de Fermata oraz Blaise Pascala. Z tego powodu, początkowo teoria prawdopodobieństwa zajmowała się niemal wyłącznie zjawiskami dyskretnymi i używała metod kombinatorycznych. Zmienne ciągłe zostały wprowadzone do teorii prawdopodobieństwa znacznie później. Za początek stworzenia współczesnej teorii prawdopodobieństwa powszechnie uważa się jej aksjomatyzację, której w 1933 dokonał Andriej Kołmogorow. Współczesna teoria prawdopodobieństwa jest ściśle związana z teorią miary.
Pomimo że wynik pojedynczego rzutu monetą lub kością do gry często z praktycznego punktu widzenia można uważać za nieprzewidywalny, jeżeli eksperyment taki powtórzony zostaje wielokrotnie, mogą pojawić się pewne prawidłowości i wzory statystyczne, które można badać i przewidzieć. Dwa przykłady takich prawidłowości, i kluczowe osiągnięcia rachunku prawdopodobieństwa, to prawo wielkich liczb oraz centralne twierdzenie graniczne.

DEFINICJA PRAWDOPODOBIEŃSTWA
Prawdopodobieństwem nazywamy dowolną funkcję P o wartościach rzeczywistych, określoną na σ-ciele zdarzeń , spełniającą warunki:
1. dla każdego ;
2. ;
3. Jeśli oraz dla , to

Warunki (1-3) zostały sformułowane przez Kołmogorowa w roku 1933 jako aksjomaty teorii prawdopodobieństwa. Matematyczny model doświadczenia losowego to trójka

gdzie P jest prawdopodobieństwem, określonym na pewnym σ-ciele F podzbiorów zbioru zdarzeń elementarnych omega. Trójkę tę nazywamy przestrzenią probabilistyczną.

Schemat Bernoulliego

Wśród doświadczeń wieloetapowych na szczególną uwagę zasługuję te, które polegają na n-krotnym powtórzeniu, w tych samych warunkach i niezależnie od siebie doświadczenia losowego, kończącego się tylko jednym z dwóch możliwych wyników. Takie doświadczenie nazywamy próbą Bernoullioego. Przykładem próby Bernoulliego jest: rzut monetą (orzeł, reszka), kupno losu na loterii (los wygrany, los przegrany).
Wielokrotne powtórzenie próby nazwiemy niezależnymi, jeśli pojawienie się dowolnych wyników w jednej próbie nie zmienia prawdopodobieństwa pojawienia się wyników przy pozostałych próbach.
Jeżeli przeprowadzimy n niezależnych i identycznych doświadczeń, w których są tylko dwa możliwe wyniki, to taki ciąg powtórzeń tego samego doświadczenia nazywamy schematem Bernoulliego. W schemacie tym jedno ze zdarzeń elementarnych nazywamy sukcesem, a drugie porażką.
W schemacie n prób Bernoulliego prawdopodobieństwo Pn(k) otrzymania dokładnie k sukcesów wyraża się wzorem:

,
gdzie p jest prawdopodobieństwem sukcesu, zaś q = 1 - p prawdopodobieństwem porażki w próbie Bernoulliego, przy czym 0 < p < 1, k = 0, 1, 2, ..., n.

Najbardziej prawdopodobna liczba sukcesów w schemacie Bernoulliego
Jeśli (n + 1)p nie jest liczbą całkowitą, to najbardziej prawdopodobną liczbą sukcesów w schemacie n prób Bernoulliego, jest największa liczba całkowita mniejsza od (n + 1)p. Jeśli natomiast (n + 1)p jest liczbą całkowitą, to najbardziej prawdopodobne są dwie wartości: (n + 1)p - 1 oraz (n + 1)p.

Test z http://wazniak.mimuw.edu.pl/index.php?title=Rachunek_prawdopodobie%C5%84stwa_i_statystyka/Test_5:_Prawdopodobie%C5%84stwo_warunkowe_i_niezale%C5%BCno%C5%9B%C4%87

Układy równań liniowych

Układ równań liniowych – koniunkcja pewnej liczby (być może nieskończonej[1]) równań liniowych, czyli równań pierwszego rzędu. Teoria układów równań liniowych jest działem algebry liniowej leżącej u podstaw nowoczesnej matematyki. Algorytmami obliczeniowymi zajmuje się dział nazywany numeryczna algebra liniowa, same zaś metody odgrywają ważną rolę w inżynierii, fizyce, chemii, informatyce i ekonomii. Częstokroć aproksymuje (przybliża) się bardziej skomplikowane układy równań nieliniowych (opisujące modele matematyczne, czy symulacje komputerowe) dużo prostszymi układami równań liniowych (tzw. linearyzacja). Układy równań liniowych rozpatruje się najczęściej nad ciałami (np. liczbami wymiernymi, rzeczywistymi, czy zespolonymi); choć ma to sens już w przypadku pierścieni (np. liczb całkowitych), to rozwiązywanie takich układów nastręcza znacznie więcej trudności (w szczególności oznacza to badanie modułów zamiast przestrzeni liniowych, zob. uogólnienia). W dalszej części przyjmuje się, że wszystkie współczynniki należą do ustalonego ciała.
Motywacje
W geometrii euklidesowej można rozpatrywać miejsca geometryczne wyznaczone przez dane dwie proste na płaszczyźnie – mogą one wyznaczać prostą, punkt lub nie wyznaczać żadnego miejsca geometrycznego; odpowiada im odpowiednio nieskończony zbiór elementów, zbiór złożony z pojedynczego elementu lub zbiór pusty. Wprowadzenie na płaszczyźnie układu współrzędnych umożliwia algebraizację tego zadania: proste zadane są za pomocą równań liniowych, zaś miejsce geometryczne wyznaczone przez te proste odpowiada zbiorowi elementów spełniających wszystkie równania jednocześnie.
Jeśli w układzie współrzędnych kartezjańskich proste zadane są równaniami

oraz

to ich jedyny punkt wspólny (x0,y0) ma współrzędne (2,3) co łatwo sprawdzić wprost:


To że jest to jedyny punkt wynika z faktu, iż proste te nie są równoległe. Zwyczajowo równania prostych zapisuje się bezpośrednio jedno pod drugim i spina klamrą:
nazywając je układem równań liniowych, zaś zbiór elementów spełniających każde równanie z osobna (odpowiadający punktom wspólnym prostych) – jego rozwiązaniami.

Rozwiązaniem układu równań x-y=-1 oraz 3x+y=9 jest para uporządkowana (2,3) gdyż podstawienie do równań poprzednika tej pary za x i jej następnika za y da dwie tożsamości.







Rozwiązania
Rozwiązaniem U nazywa się dowolny ciąg liczb ri który po podstawieniu za xj będzie spełniał każde z równań U. Układ, który nie ma rozwiązań, nazywa się sprzecznym; jeżeli zbiór rozwiązań układu jest niepusty, to nazywa się go niesprzecznym. Układ niesprzeczny, który ma jedno i tylko jedno rozwiązanie, nazywa się oznaczonym; układy o więcej niż jednym rozwiązaniu nazywa się nieoznaczonymi – w przypadku układów liniowych nad ciałami nieskończonymi (takimi jak liczby wymierne, liczby rzeczywiste, czy liczby zespolone) oznacza to, że układ ma nieskończenie wiele rozwiązań.
Wskazówkę co do ogólnej liczby rozwiązań układu daje już sama jego postać:
układ niedookreślony, który ma mniej równań niż niewiadomych, zwykle jest nieoznaczony;
układ nadokreślony mający więcej równań niż niewiadomych, zazwyczaj jest sprzeczny;
układ, który ma tyle równań co niewiadomych, często ma jedno rozwiązanie.
Przypadki te obrazują następujące wykresy dla układów równań liniowych dwóch zmiennych:

Zbiór rozwiązań dwóch równań liniowych o trzech zmiennych zwykle tworzy prostą (przestrzeń jednowymiarową).

Układ równań liniowych o trzech zmiennych określa zbiór płaszczyzn - dowolny ich punkt przecięcia (o ile istnieje) jest rozwiązaniem układu.

Metoda Monte Carlo - Film

Aproksymacja

Aproksymacja – proces określania rozwiązań przybliżonych na podstawie rozwiązań znanych, które są bliskie rozwiązaniom dokładnym w ściśle sprecyzowanym sensie. Zazwyczaj aproksymuje się byty (np. funkcje) skomplikowane bytami prostszymi. Często stosowana w przypadku szukania rozwiązań dla danych uzyskanych metodami empirycznymi, które mogą być obarczone błędami.

APROKSYMACJA FUNKCJI
Aproksymacje można wykorzystać w sytuacji, gdy nie istnieje funkcja analityczna pozwalająca na wyznaczenie wartości dla dowolnego z jej argumentów, a jednocześnie wartości tej nieznanej funkcji są dla pewnego zbioru jej argumentów znane. Mogą to być na przykład wyniki badań aktywności biologicznej dla wielu konfiguracji leków. Do wyznaczenia aproksymowanej aktywności biologicznej nieznanego leku można wówczas zastosować jedną z wielu metod aproksymacyjnych.
Aproksymowanie funkcji może polegać na przybliżaniu jej za pomocą kombinacji liniowej tzw. funkcji bazowych. Od funkcji aproksymującej, przybliżającej zadaną funkcję nie wymaga się, aby przechodziła ona przez jakieś konkretne punkty, tak jak to ma miejsce w interpolacji. Z matematycznego punktu widzenia aproksymacja funkcji f w pewnej przestrzeni Hilberta H jest zagadnieniem polegającym na odnalezieniu pewnej funkcji gdzie G jest podprzestrzenią H tj. takiej, by odległość (w sensie obowiązującej w H normy) między f a g była jak najmniejsza. Funkcja aproksymująca może wygładzać daną funkcję (gdy funkcja jest gładka, jest też różniczkowalna).

Aproksymacja funkcji powoduje pojawienie się błędów, zwanych błędami aproksymacji. Dużą zaletą aproksymacji w stosunku do interpolacji jest to, że aby dobrze przybliżać, funkcja aproksymująca nie musi być wielomianem bardzo dużego stopnia (w ogóle nie musi być wielomianem). Przybliżenie w tym wypadku rozumiane jest jako minimalizacja pewnej funkcji błędu. Prawdopodobnie najpopularniejszą miarą tego błędu jest średni błąd kwadratowy, ale możliwe są również inne funkcje błędu, jak choćby błąd średni.
Istnieje wiele metod aproksymacyjnych. Jednymi z najbardziej popularnych są: aproksymacja średniokwadratowa i aproksymacja jednostajna oraz aproksymacja liniowa, gdzie funkcją bazową jest funkcja liniowa.
Wiele z metod aproksymacyjnych posiada fazę wstępną, zwaną również fazą uczenia oraz fazę pracy. W fazie wstępnej, metody te wykorzystując zadane pary punktów i odpowiadających im wartości aproksymacyjnych niejako „dostosowują” swoją strukturę wewnętrzną zapisując dane, które zostaną wykorzystane później w fazie pracy, gdzie dla zadanego punktu dana metoda wygeneruje odpowiadającą mu wartość bądź wartości aproksymowane. Funkcja aproksymująca może być przedstawiona w różnej postaci. Najczęściej jest to postać:
- wielomianu (tzw. aproksymacja wielomianowa),
- funkcji sklejanych,
- funkcji matematycznych uzyskanych na drodze statystyki matematycznej (przede wszystkim regresji),
- sztucznych sieci neuronowych.
Funkcje aproksymujące w postaci wielomianu i funkcji sklejanych można wykorzystać jedynie wtedy, gdy funkcja aproksymowana jest w postaci jednej zmiennej.

ZADANIE NAJLEPSZEJ APROKSYMACJI
Niech dana będzie przestrzeń liniowa X z normą i niech będzie podprzestrzenią liniową X skończonego wymiaru. Zadanie najlepszej aproksymacji polega na znalezieniu takiego (elementu najlepszej aproksymacji dla danego ), że zachodzi:

Należy przez to rozumieć, że element v* jest elementem "najbliższym" do aproksymowanego x spośród wszystkich elementów .
Zadanie najlepszej aproksymacji jest zawsze rozwiązywalne tzn. dla każdego istnieje element najlepszej aproksymacji v*, ale niekoniecznie jest on jedyny. Należy zauważyć, że element najlepszej aproksymacji zależy od normy, jaka została przyjęta w przestrzeni X.

ZADANIE NAJLEPSZEJ APROKSYMACJI W PRZESTRZENIACH UNITARNYCH
Niech X będzie przestrzenią z iloczynem skalarnym i niech norma w X będzie generowana tym iloczynem:
Wtedy element najlepszej aproksymacji jest jedyny i jest określony następującą tożsamością